Tree Kernels In SVM-lighT

by Alessandro Moschitti

The latest version of the software is SVM-lighT-TK 1.5

Syntactic parsers are among of the most useful tools for Natural Language Processing (NLP) applications. However, how to exploit the syntactic parse tree information in NLP tasks is considered an open problem. For example, the learning models for automatic Word Sense Disambiguation or Coreference Resolution would benefit from syntactic tree features but their design and selection is not an easy task.

Convolution kernels (see Kernel philosophy in NLP) are an alternative to the explicit feature design. They measure similarity between two syntactic trees in terms of their sub-structures (e.g. [Collins and Duffy, 2002]). These approaches have given optimal results [Moschitti, 2004] when introducing syntactic information in the task of Predicate Argument Classification.

Suppose we want to measure the similarity between the parse trees of two noun phrases: "a dog" and "a cat". The idea of behind syntactic tree kernels is graphically described by the following figure:

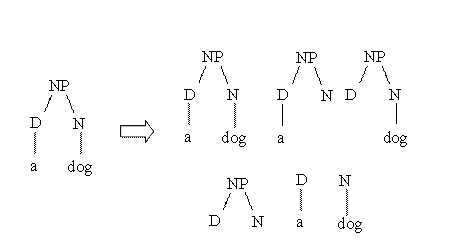
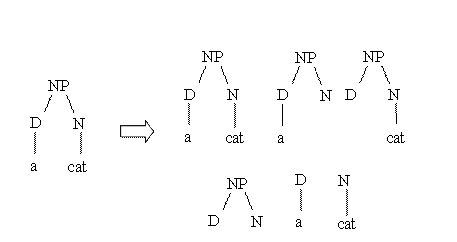
As 3 structures (out of 5) are completely identical the similarity is equal to 3.

This kind of similarity has been shown useful to improve the ranking of the m best syntactic parse trees [Collins and Duffy, 2002]. Other interesting applications concern the classification of predicate argument structures annotated in PropBank and Question Classification [Zhang and Lee, 2003; Moschitti, ECML 2006]. To describe the linguistic phenomenon of the former task, i.e. the syntactic/semantic relation between a predicate and the semantic roles of its arguments, we need to extract features from some subparts of a syntactic tree. For example given the following sentence:

Paul gives a talk in Rome

The Predicate argument annotation in PropBank is:

[ Arg0 Paul] [ Predicate gives] [ Arg1 a talk] [ ArgM in Rome]

The syntactic tree may be:

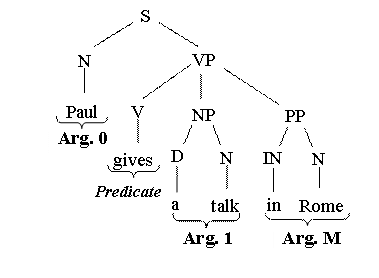
To select syntactic information related to a particular argument type we could use the corresponding subtree, i.e.:

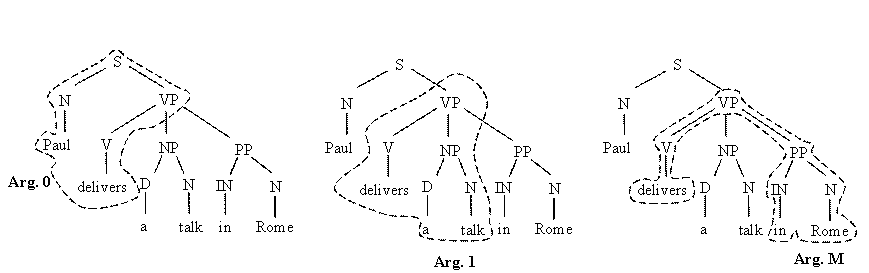
Tree-Kernels measure the similarity between arguments whereas the kernel-based algorithms (e.g. SVMs) automatically select the substructures that better describe the argument type.

How to use SVM-lighT-TK

The tree kernel has been encoded inside the well known SVM-light software written by Thorsten Joachims (www.joachims.org). The input format and the new options are compatible with those of the original SVM-light 5.01. Moreover, combination models between tree kernels and feature vectors are available.

Software Features

- Fast Kernel Computation [Moschitti, EACL 2006] (already available since the previous version).

- Vector sets, multiple feature vectors over multiple feature spaces can be specified in the input. This allows us to use different kernels with different feature subsets. Given two objects, O₁ and O₂, described by two sets of feature vectors, and , several kernels can be defined:

- Tree forests, a set of trees over multiple feature spaces can be specified in the input. This allows us to use a set of different structured features, e.g. it is possible to extract different portions from a parse tree and combine the different contributions. This limits the sparseness of the kernels applied to the whole tree. Given two objects, O₁ and O₂, described by two sets of trees, and , several kernels can be defined on:

- Two types of tree kernels:

1. SubSet Tree kernel (SST) [Collins and Duffy, 2002; Moschitti, EACL 2006]

2. Subtree kernel (ST) [Vishwanathan and Smola, 2001; Moschitti, EACL 2006]

- Embedded combinations of Trees and vectors:

1. sequential summation, the kernels between corresponding pairs of trees and/or vectors in the input sequence are summed together. The t parameter rules the contributions of tree kernels K_t with respect to the feature vector kernel k_b. Each of the two types of kernels can or cannot be normalized according to a command line parameter. More formally:

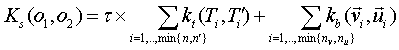K_tcan be either the SST or the ST kernel whereas k_b can be one of the traditional kernels on feature vectors, e.g. gaussian or polynomial kernel.

2. all vs all summation, each tree and vector of the first object are evaluated against each tree and vector of the second object:

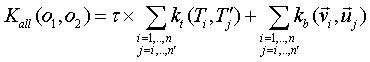
Data Format

The data format is the same as SVM-Light-TK-1.2. I improved the generality of the tree please read the explanation of the software below.
The major difference is the use of more general trees and the possibility to execute the Partial Tree Kernel, (PTK) [Moschitti, 2006].

You can use any tree for example the simple tree below

         A
      /   | \
     a   b c

can be represented with the following syntax:

(A (a)(b)(c))

Pay attention!! you cannot write such tree as (A a b c).

More in detail the input takes sets of objects:

<set-of-vectors> ::= <vector> |<vector><blank><begin-vector><blank><vector><blank>..<end-vector>

<set-of-trees> ::= <begin-tree><blank><tree><blank>..<begin-tree><blank><tree><blank><end-tree>

<trees-and-vectors>::= <set-of-trees><blank><set-of-vectors>

<begin-tree> ::="|BT|"

<end-tree> ::="|ET|"

<begin-vector>::="|BV|"

<end-vector> ::="|EV|"

<full-tree> ::= (<root><blank><full-tree>..<full-tree>) | (<root><blank><leaf>)

<blank> ::= " " (i.e. one space)

where <string> does not contain space, left and right parentheses, i.e. "(" and ")", whereas <tree> defines the usual Penn Treebank format. Note that (a) two begin trees, i.e. ".. |BT| |BT| .." encode the empty tree (useful as placeholder), (b) two begin vectors, i.e. ".. |BV| |BV| .." encode the empty vector and (c) the sequence ".. |ET| |BV| .." is used to specify that the first vector (after trees) is empty.

For example, if we liked to experiment with different trees for question classification, given the question "What does S.O.S stand for?", we may use the following forest:

1 |BT| (SBARQ (WHNP (WP What))(SQ (AUX does)(NP (NNP S.O.S.))(VP (VB stand)(PP (IN for))))(. ?)) |BT| (BOW (What *)(does *)(S.O.S. *)(stand *)(for *)(? *)) |BT| (BOP (WP *)(AUX *)(NNP *)(VB *)(IN *)(. *)) |BT| (PAS (ARG0 (R-A1 (What *)))(ARG1 (A1 (S.O.S. NNP)))(ARG2 (rel stand))) |ET|

where the four different trees are: the question parse tree, the BOW tree (used to simulate the bag-of-words), the BOP tree (used to simulate the bag-of-POS-tags) and the predicate argument tree (i.e. the PAS defined in [Moschitti et al., ECML-MLG 2006])

We can add trees with different feature vectors. For example suppose we want to implement a re-ranker based on tree kernel and flat features. We need to compare pairs of instances. The following line contains a pair of PASs and a pair of feature vectors that correspond to two target predicate argument structures. These are needed for learning of a re-ranker for Semantic Role Labeling systems [Moschitti et al., CoNLL 2006].

-1 |BT| (TREE (ARG0 (A1 NP))(ARG1 (AM-NEG RB))(ARG2 (rel fall))(ARG3 (AM-TMP NNP))(ARG4 (AM-TMP SBAR))(ARG5 null)(ARG6 null)) |BT| (TREE (ARG0 (A1 NP))(ARG1 (AM-NEG RB))(ARG2 (rel fall))(ARG3 (A4 RP))(ARG4 (AM-TMP NNP))(ARG5 (AM-TMP SBAR))(ARG6 null)) |ET| 1:1 21:2.742439465642236E-4 23:1 30:1 36:1 39:1 41:1 46:1 49:1 66:1 152:1 274:1 333:1 |BV| 2:1 21:1.4421347148614654E-4 23:1 31:1 36:1 39:1 41:1 46:1 49:1 52:1 66:1 152:1 246:1 333:1 392:1 |EV|

In case we liked to use only feature vectors we could write them as follows:

-1 1:1 21:2.742439465642236E-4 23:1 30:1 36:1 39:1 41:1 46:1 49:1 66:1 152:1 274:1 333:1 |BV| 2:1 21:1.4421347148614654E-4 23:1 31:1 36:1 39:1 41:1 46:1 49:1 52:1 66:1 152:1 246:1 333:1 392:1 |EV|

However, the original SVM-light input format can be used without any changes as the next two lines associated with two instances illustrate:

-1 1:1 21:2.742439465642236E-4 23:1 30:1 36:1 39:1 41:1 46:1 49:1 66:1 152:1 274:1 333:1

+1 2:1 21:1.4421347148614654E-4 23:1 31:1 36:1 39:1 41:1 46:1 49:1 52:1 66:1 152:1 246:1 333:1 392:1

Important: follow the syntax of trees defined by <tree> (e.g. there is no space between two parenthesis). Moreover, the expected input is a parse-tree this means that a pre-terminal (the lowest non-terminal in the tree) is always followed by only one leaf.

Commands

The "svm_classify" and the "svm_learn" commands maintain the original svm-light format:

usage: svm_learn [options] example_file model_file

Arguments:

example_file-> file with training data

model_file -> file to store the learned decision rules in

usage: svm_classify [options] example_file model_file

Arguments:

example_file-> file with testing data

model_file -> file to retrieve the learned decision rules

The new options are shown below (in blue colour):

Kernel options:

-t int -> type of kernel function:

0: linear (default)

1: polynomial (s a*b+c)^d

2: radial basis function exp(-gamma ||a-b||^2)

3: sigmoid tanh(s a*b + c)

4: user defined kernel from kernel.h

5: combination of forest and vector sets according to W, V, S, C options

11: re-ranking based on trees (each instance must have two trees)

12: re-ranking based on vectors (each instance must have two vectors)

13: re-ranking based on both tree and vectors (each instance must have two trees and two vectors)

-W [S,A] -> a tree kernel is applied to the sequence of trees of two input forests and the results are summed;

-> with an "A", a tree kernel is applied to all tree pairs from the two forests (default "S")

-V [S,A] -> same as before but sequences of vectors are used (default "S" and the type of vector-based kernel is specified by the option -S)

-S [0,4] -> kernel to be used with vectors (default polynomial of degree 3, i.e. -S = 1 and -d = 3)

-C [*,+,T,V] -> combination operator between forests and vectors (default 'T')

-> "T" only the contribution from trees is used

-> "V" only the contribution from feature vectors is used

-> "+" or "*" sum or multiplication of the contributions from feature vectors and trees (default 'T')

-T float -> multiplicative constant for the contribution of tree kernels when -C = "+", i.e. K = tree-forest-kernel*r + vector-kernel (default 1)

-D [0,1] -> 0, SubTree kernel or 1, SubSet Tree kernels (default 1)

-F [0,1,2,3,4,6]-> 0 = ST kernel, 1 = SST kernel, 2 = SST-bow, 3 = PT kernel (default 1), 6=STRING kernel

-M float -> Mu decay factor for PT kernel (default 0.4)

-L float -> decay factor in tree kernels (default 0.4)

-N [0,3] -> 0 = no normalization, 1 = tree normalization, 2 = vector normalization and, 3 = normalization of both trees and vectors. The normalization is applied to each individual tree or vector (default 3).

-u string -> parameter of user defined kernel

-d int -> parameter d in polynomial kernel

-g float -> parameter gamma in rbf kernel

-s float -> parameter s in sigmoid/poly kernel

-r float -> parameter c in sigmoid/poly kernel

To obtain the sequential summation K_s (of tree and vector kernels) previously defined, we can set the option "-t 5 -T 1 -W S -V S -C +". Considering the default values, this is equivalent to use "-t 5 -C +".

-F decides the type of tree kernel
-1 // Moschtti et al. 2007

0 // VISHTANAM and SMOLA 2002

1 // COLLINS and DUFFY 2002

2 // ZHANG, 2003

3 // Moschitti, ECML 2006

4 // something ibrid

6 // STRING_KERNEL, Taylor and Cristianini book 2004, just put a fake root and only one level of children, i.e., the elements of your sequence.

Example of New Options

./svm_learn -t 5 example_file model_file /* the subset-tree kernel alone is used, if the forest contains only a tree, the classic tree kernel is computed */

./svm_learn -t 5 -C V example_file model_file /* the default polynomial kernel is used on the pairs from vector sequences */

./svm_learn -t 5 -C V -V A example_file model_file /* the default polynomial kernel is used on the pairs from

vector sequences. The pairs are built by combining each element of the first sequence with each element of the second sequence */

./svm_learn -t 5 -C + -S 1 -d 5 example_file model_file /* the sequential summation of trees, using SST kernel, is summed to the sequential summation of vectors, using a polynomial kernel with degree = 5. The contribution of tree kernels is multiplied by t (i.e. default 1) */

./svm_learn -t 5 -C + -D 0 -S 1 example_file model_file /* the sequential summation of trees, using the ST kernel (-D 0), is summed to the sequential summation of vectors, using polynomial kernel with degree = 5 */

./svm_learn -t 12 example_file model_file /* a re-ranker over a pair of trees and a pair of vectors is applied*/

./svm_learn example_file model_file /* original SVM-light linear kernel "-t 0". The input can be provided in the new style or in the old SVM-light format*/

Download SVM-LIGHT-TK 1.5

- Source code (It is available with the make files for Windows DevC++ and Linux gcc)

- Example data (it contains the PropBank Argument 0 as positive class and Argument 1 as negative class)

It is possible to design our own kernel by using weights for both trees and vectors and combining them in very different way as the following example illustrates:

- kernel.h

Download SVM-LIGHT-TK 1.2

This version does not contain PTK, it should not be faster than the new SVM-Light-TK1.5. Anyway if you do not need general trees and PTK, you may want to use this one.

- Source code (It is available with the make files for Windows DevC++ and Linux gcc)

Download SVM-LIGHT-TK 1.0

All the options of previous SVM-LIGHT-TK version have been integrated in SVM-LIGHT-TK 1.2.

However, the use of forest and vector set make slightly slower the new version so if you just need a fast computation of one tree kernel.

Note that the data format is different so please watch the page:

SVM-LIGHT-TK1.0

Software References

Please refer to the tree-kernel software as one of the following

[Moschitti, 2006], Alessandro Moschitti, Efficient Convolution Kernels for Dependency and Constituent Syntactic Trees. In Proceedings of the 17th European Conference on Machine Learning, Berlin, Germany, 2006.

[Moschitti, 2004], Alessandro Moschitti. A study on Convolution Kernels for Shallow Semantic Parsing. In proceedings of the 42-th Conference on Association for Computational Linguistic (ACL-2004), Barcelona, Spain, 2004.

[Moschitti, 2006], Alessandro Moschitti, Making tree kernels practical for natural language learning. In Proceedings of the Eleventh International Conference on European Association for Computational Linguistics, Trento, Italy, 2006.

along with the SVM-light software as

[Joachims, 1999], Thorsten Joachims. Making large-scale SVM learning practical. In B. Scholkopf, C. Burges, and A. Smola, editors, Advances in Kernel Methods - Support Vector Learning, 1999.

General References

[Collins and Duffy, 2002], Michael Collins and Nigel Duffy. New ranking algorithms for parsing and tagging: Kernels over discrete structures, and the voted perceptron. In ACL02, 2002.

[Moschitti, ECML 2006], Alessandro Moschitti, Efficient Convolution Kernels for Dependency and Constituent Syntactic Trees. In Proceedings of the 17th European Conference on Machine Learning, Berlin, Germany, 2006.

[Moschitti et al., ECML-MLG 2006], Alessandro Moschitti, Daniele Pighin, and Roberto Basili, Tree Kernel Engineering for Proposition Re-ranking, In Proceedings of Mining and Learning with Graphs (MLG 2006), Workshop held with ECML/PKDD 2006, Berlin, Germany, 2006.

[Moschitti et al., CoNLL 2006], Alessandro Moschitti, Daniele Pighin and Roberto Basili. Semantic Role Labeling via Tree Kernel joint inference. In Proceedings of the 10th Conference on Computational Natural Language Learning, New York, USA, 2006.

[Vishwanathan and Smola, 2002], S.V.N. Vishwanathan and A.J. Smola. Fast kernels on strings and trees. In Proceedings of Neural Information Processing Systems, 2002.

[Zhang and Lee, 2003], Zhang, D., Lee, W.S.: Question classification using support vector machines. In: Proceedings of SIGIR'03, 2003.

Back to Home

Top of the Page

Maintained by Alessandro Moschitti moschitti[at]dit.unitn.it

Tree Kernels In SVM-lighT

by Alessandro Moschitti

The latest version of the software is SVM-lighT-TK 1.5

How to use SVM-lighT-TK

Software Features

Data Format

Commands

Example of New Options

Download SVM-LIGHT-TK 1.5

Download SVM-LIGHT-TK 1.2

Download SVM-LIGHT-TK 1.0

Download SVM-LIGHT-TK 1.0

More documentation examples are available at the link of my Tutorial on kernels at

Software References

Please refer to the tree-kernel software as one of the following

along with the SVM-light software as

General References